This week’s Riddler Classic is a question about large numbers of attempts at a very unlikely thing.
Graydon is about to depart on a boating expedition that seeks to catch footage of the rare aquatic creature, F. Riddlerius. Every day he is away, he will send a hand-written letter to his new best friend, David Hacker. But if Graydon still has not spotted the creature after $n$ days (where $n$ is some very, very large number), he will return home.
Knowing the value of $n$, Graydon confides to David there is only a 50 percent chance of the expedition ending in success before the $n$ days have passed. But as soon as any footage is collected, he will immediately return home (after sending a letter that day, of course).
On average, for what fraction of the $n$ days should David expect to receive a letter?
My solution:
[Show Solution]
We will assume the probability of spotting the creature on any given day is $p$ and is independent one day to the next. We are told the probability the expedition will fail is $\frac{1}{2}$. This occurs when the creature is not observed for $n$ days. This event has probability $(1-p)^n$. Therefore, we have
\[
(1-p)^n = \frac{1}{2}
\]We can solve this equation for $p$ and we find
\[
p = 1-2^{-1/n}
\]
If Graydon sends $k$ letters (with $1\leq k \leq n-1$), this means that the creature was spotted on the $k^\text{th}$ day, after not being spotted for the first $k-1$ days. The probability of this event is $p(1-p)^{k-1}$. If $n$ letters are sent, then either the creature was spotted on the last day (probability $p(1-p)^{n-1}$), or the creature was not spotted at all (probability $(1-p)^n$). Let the average fraction of days where a letter is received be $A$. This quantity is equal to the expected number of letters received divided by $n$. Therefore, we obtain:
\[
A = \frac{1}{n} \sum_{k=1}^n k p(1-p)^{k-1} + (1-p)^n
\]We can evaluate this sum in closed form, and we obtain
\[
A = \frac{1-(1-p)^n}{n p}
\]Substituting what we found for $p$, we obtain
\[
A = \frac{1}{2n(1-2^{-1/n})}
\]We are told that “$n$ is very very large”, so it makes sense to examine what happens as $n\to\infty$. Doing so, we observe that $A$ tends to a constant:
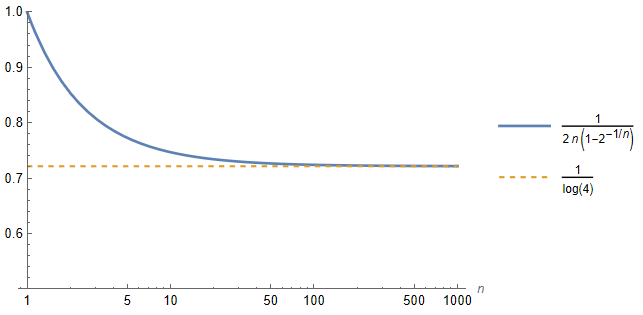
With a bit of work, we can actually evaluate the limit exactly:
\[
\lim_{n\to\infty} \frac{1}{2n(1-2^{-1/n})}
= \frac{1}{\log (4)} \approx 0.721348
\]So, on average, David should expect to receive a letter on approximately 72.1% of the days.
Alternative approach
A slightly faster way to get to the same answer is to realize that if $(1-p)^n=\frac{1}{2}$ and $n$ is “very very large”, then it must be true that $p$ is “very very small”. Specifically, if we recall the fact that
\[
\lim_{n\to\infty} \left(1+\frac{x}{n}\right)^n = e^x
\]Then we can rearrange:
\[
(1-p)^n = \left(1 + \frac{(-np)}{n}\right)^n
\]So if $n\to\infty$, we conclude that $e^{-np} \to \frac{1}{2}$, or that $np \to \log(2)$. Therefore, we can return to our original expression for $A$ and substitute $(1-p)^n \to \tfrac{1}{2}$ and $np\to \log(2)$ and we find:
\[
A = \frac{1-(1-p)^n}{n p} \to \frac{1}{\log(4)}
\]which is the same thing we found using the first approach.
